d <- tibble(id = c("01", "02", "03", "04", "05", "06", "07", "08"),
age = c(12, 13, 15, 16, 18, 20, 22, 24),
time = c(2, 1, 4, 3, 6, 5, 3, 4)
)Übung 13
Korrelation
Hinweis: Diese Übung verwendet das Package {tidyverse}, das Laden von webr kann daher etwas länger dauern als sonst.
Aufgaben
Hinweise:
- Die Formelsammlung zu dieser Übung finden Sie auf OLAT.
- Die Tabelle für die Standardnormalverteilung finden Sie hier.
- Die Tabelle für die t-Verteilung finden Sie hier.
- Die Tabelle für die \(\chi^2\)-Verteilung finden Sie hier.
Aufgabe 13.1
- Wie unterscheiden sich die Kreuzproduktsumme, die Kovarianz und die Produkt-Moment-Korrelation?
Lösung Aufgabe 13.1a
Die Kreuzproduktsumme hängt von der Anzahl der Merkmalsträger ab, die Kovarianz nicht. Die Kovarianz erhält man, indem man die Kreuzproduktsumme durch die Anzahl der Merkmalsträger dividiert. Die Kovarianz ist somit die mittlere Kreuzproduktsumme. Die Korrelation ist eine standardisierte Kovarianz, die durch das Produkt der Standardabweichungen geteilt wird.
- Welchen Wert hat die Kovarianz, wenn eine der beiden beteiligten Variablen eine Varianz von 0 hat?
Lösung Aufgabe 13.1b
In diesem Fall beträgt die Kovarianz ebenfalls 0, da alle Werte der Variablen, deren Varianz 0 beträgt, mit deren Mittelwert identisch sind. Deshalb sind auch alle Abweichungen vom Mittelwert 0. Somit müssen auch alle Abweichungsprodukte 0 betragen.
- Wie verändert sich die Kovarianz, wenn man zu allen Werten auf der Variablen X eine Konstante von 3 und zu allen Werten auf der Variablen Y eine Konstante von 5 hinzuaddiert?
Lösung Aufgabe 13.1c
Die Kovarianz ändert sich durch die Addition von Konstanten nicht. Dasselbe gilt somit auch für die Korrelation. Grafisch “verschiebt” sich die Punktewolke lediglich, der Zusammenhang ändert sich dadurch aber nicht.
Aufgabe 13.2
- Ist der Zusammenhang zweier Variablen positiv, so sind auch alle Kreuzprodukte positiv.
- Bei einem perfekten negativen linearen Zusammenhang zwischen X und Y liegen alle Punkte im Streudiagramm auf einer Linie.
- Wenn x-Werte, die oberhalb des Mittelwertes von X liegen, mit y-Werten einhergehen, die unterhalb des Mittelwerts von Y liegen (und umgekehrt), so liegt ein negativer Zusammenhang vor.
- Die Kreuzproduktsumme kann kleiner als 0 werden.
- Die Kovarianz kann kleiner als 0 werden.
- Die Korrelation kann grösser als 1 werden.
Aufgabe 13.3
Bei acht Jugendlichen und jungen Erwachsenen wurde das Alter und der tägliche Medienkonsum in Stunden erfasst.
| ID | Alter | Medienkonsum in Stunden pro Tag |
|---|---|---|
| 1 | 12 | 2 |
| 2 | 13 | 1 |
| 3 | 15 | 4 |
| 4 | 16 | 3 |
| 5 | 18 | 6 |
| 6 | 20 | 5 |
| 7 | 22 | 3 |
| 8 | 24 | 4 |
- Berechnen Sie die Kreuzproduktsumme, die Kovarianz und die Produkt-Moment-Korrelation.
Wie gehe ich vor?
Berechnen Sie den Mittelwert und die Standardabweichung der beiden Variablen “Alter” und “Medienkonsum”.
Berechnen Sie für jede Person die Abweichung vom Mittelwert für beide Variablen und berechnen Sie daraus das Produkt: \((x-\overline x) \cdot (y-\overline y)\). Hier könnte es hilfreich sein, eine Tabelle zu erstellen.
Berechnen Sie daraus die Kreuzproduktsumme, dann die Kovarianz und daraus die Korrelation.
Lösung Aufgabe 13.3a
Mittelwert und Standardabweichung von X ergibt:
\(\overline x=17.5\), \(s_x=4\)
Mittelwert und Standardabweichung von Y ergibt:
\(\overline y=3.5\), \(s_y=1.5\)
| ID | \(x\) | \(y\) | \(x-\overline x\) | \(y-\overline y\) | \((x-\overline x) \cdot (y-\overline y)\) |
|---|---|---|---|---|---|
| 1 | 12 | 2 | -5.5 | -1.5 | 8.25 |
| 2 | 13 | 1 | -4.5 | -2.5 | 11.25 |
| 3 | 15 | 4 | -2.5 | 0.5 | -1.25 |
| 4 | 16 | 3 | -1.5 | -0.5 | 0.75 |
| 5 | 18 | 6 | 0.5 | 2.5 | 1.25 |
| 6 | 20 | 5 | 2.5 | 1.5 | 3.75 |
| 7 | 22 | 3 | 4.5 | -0.5 | -2.25 |
| 8 | 24 | 4 | 6.5 | 0.5 | 3.25 |
| \(\sum\) | 140 | 28 | 0 | 0 | 25 |
| m | 17.5 | 3.5 | 0 | 0 | 3.125 |
| s | 4 | 1.5 | 0 | 0 |
Die Kreuzproduktsumme beträgt \(25\).
Die Kovarianz entspricht dem Mittelwert der Kreuzproduktsumme \(s_{xy}=\frac{25}{8}=3.125\).
Die Korrelation erhält man, wenn man die Kovarianz durch das Produkt der Streuung teilt (\(s_x \cdot s_y=4 \cdot 1.5=6\)). Die Korrelation beträgt somit \(r=\frac{3.125}{6}=0.52\).
Es handelt sich hier um einen starken positiven Zusammenhang, da der Wert über 0.5 liegt. (Achtung: In der vorherigen Version war hier fälschlicherweise von einem “mittleren positiven Zusammenhang” die Rede.)
- Berechnen Sie, ob die Korrelation auf dem 5%-Niveau signifikant von 0 verschieden ist (zweiseitiger Test).
Lösung Aufgabe 13.3b
- Empirische Prüfgrösse berechnen:
\(t=\frac{r \cdot \sqrt{n-2}}{\sqrt{1-r^2}}=\frac{0.52 \cdot \sqrt{8-2}}{\sqrt{1-0.2704}}=1.49\)
- Kritischer Wert und Anzahl Freiheitsgrade bestimmen:
\(df=n-2=6\)
\(t_{0.975;6}=2.4469\)
Die Nullhypothese kann nicht abgelehnt werden, da der kritische Wert stärker von 0 entfernt ist, als die empirische Prüfgrösse.
- Konstruieren Sie das 95%-Konfidenzintervall für \(r\).
Lösung Aufgabe 13.3c
- Transformation in \(Z_r\):
\(Z_r=0.5 \cdot \ln\frac{1+r}{1-r}=0.5 \cdot \ln\frac{1.52}{0.48}=0.576\)
- Konfidenzintervall mit \(Z_r\) und dem entsprechenden \(z\)-Wert:
Untere Grenze: \(Z_r-z_{(0.975)} \cdot \frac{1}{\sqrt{n-3}}=0.576-1.96 \cdot \frac{1}{\sqrt{5}}=-0.30\)
Obere Grenze: \(Z_r+z_{(0.975)} \cdot \frac{1}{\sqrt{n-3}}=0.576+1.96 \cdot \frac{1}{\sqrt{5}}=1.45\)
- Konfidenzintervall in \(r\) zurücktransformieren:
\(r_u=\frac{e^{2\cdot(-0.30)}-1}{e^{2\cdot(-0.30)}+1}=\frac{0.549-1}{0.549+1}=-0.29\)
\(r_o=\frac{e^{2\cdot(1.45)}-1}{e^{2\cdot(1.45)}+1}=\frac{18.17-1}{18.17+1}=0.90\)
95%-KI:\([-0.29;0.90]\)
Da das 95%-Konfidenzintervall 0 überdeckt, kann die Nullhypothese nicht abgelehnt werden.
Aufgabe 13.4
Die Korrelation zweier Variablen X und Y beträgt \(r_{xy}=0.8\). Die Streuungen betragen \(s_x=2.5\) und \(s_y=10\). Es wurden Daten von \(n=120\) Personen erhoben. Berechnen Sie die Kovarianz und die Kreuzproduktsumme.
Lösung Aufgabe 13.4
Die Korrelation wird mit dem Produkt der Standardabweichungen multipliziert.
\(s_{xy}=r_{xy} \cdot (s_x \cdot s_y)=0.8 \cdot 25=20\)
Nun kann die Kovarianz mit der Stichprobengrösse multipliziert werden.
\(KPS=s_{xy} \cdot n=20 \cdot 120=2400\)
Aufgabe 13.5
Verwenden Sie nun die Daten aus Aufgabe 13.3. Erstellen Sie in R (WebR) einen Datensatz aus den drei Variablen: z.B. id, age und time.
Zur Erinnerung: Sie können mehrere Werte als Variable speichern, indem Sie die Funktion c() nutzen. Die Variable x <- c(18, 17, 19) enthält die Werte 18, 17 und 19. Mehrere Variablen können Sie mit der Funktion tibble zu einem Datensatz zusammenfügen. Weitere Hinweise finden Sie unter Einführung in R.
Fügen Sie in die Klammer die Werte aus Aufgabe 13.3 ein und trennen Sie die Werte jeweils mit einem Komma. Erstellen Sie für jede Spalte eine Variable.
Drücken Sie Run Code.
Schauen Sie sich die Daten nun genauer an. Verwenden Sie glimpse(), um die Werte auszugeben. Berechnen Sie für die beiden metrischen Variablen den Mittelwert und die Standardabweichung.
Verwenden Sie die Namen der Objekte, die Sie zu Beginn definiert haben. Die Funktion mean(__$__)benötigt einerseits den Namen des Datensatzes, aber auch der Variable z.B. mean(d$age).
Drücken Sie Run Code.
#Datensatz anschauen
glimpse(d)
#Mittelwert und Standardabweichung berechnen
mean(d$age)
sd(d$age)
mean(d$time)
sd(d$time)
Output Aufgabe 13.5a
## Rows: 8
## Columns: 3
## $ id <chr> "01", "02", "03", "04", "05", "06", "07", "08"
## $ age <dbl> 12, 13, 15, 16, 18, 20, 22, 24
## $ time <dbl> 2, 1, 4, 3, 6, 5, 3, 4
## [1] 17.5
## [1] 4.27618
## [1] 3.5
## [1] 1.603567Nun können Sie die beiden Variablen plotten und die Korrelation ausgeben lassen. Vergleichen Sie den Output von R mit Ihren Berechnungen von Aufgabe 13.3.
Verwenden Sie wiederum die gleichen Bezeichnungen wie vorher z.B. d$age.
Drücken Sie Run Code.
#Scatterplot (Streudiagramm) anschauen
plot(d$age,d$time)
#Korrelation berechnen
cor(d$age,d$time)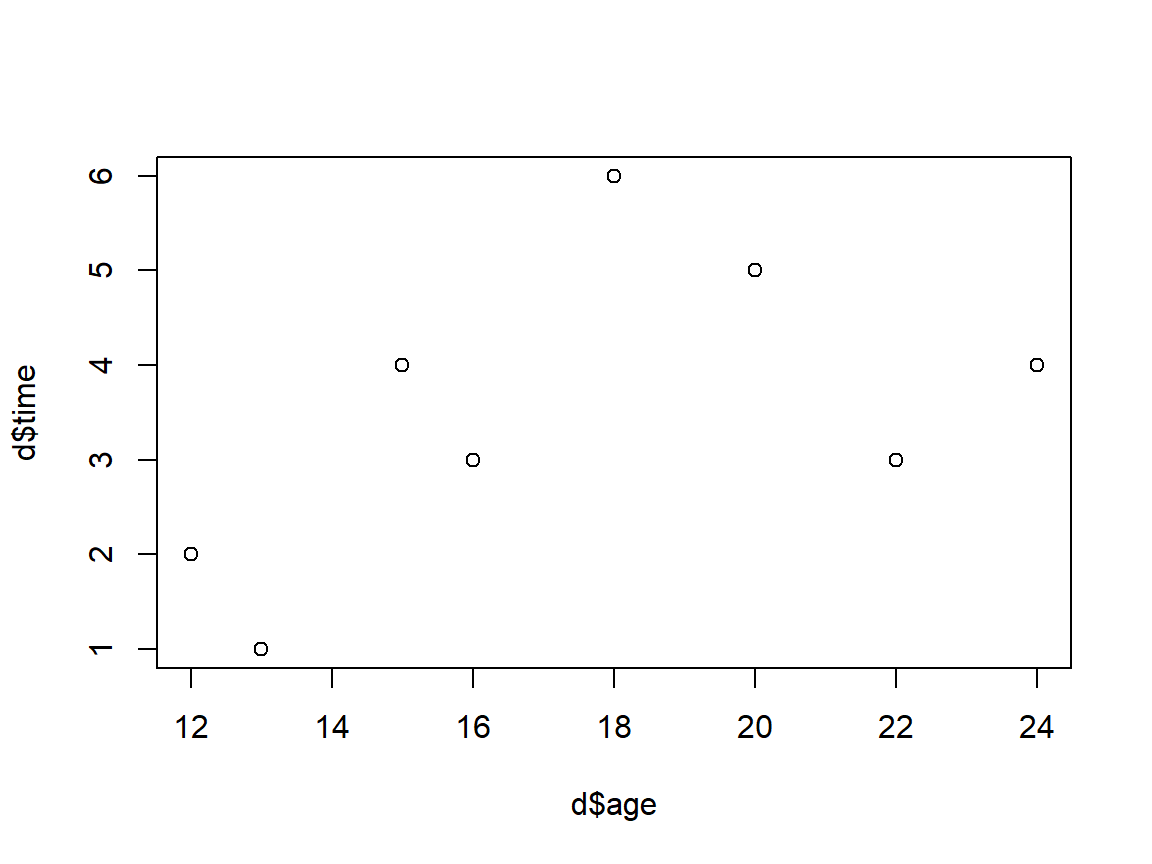
Output Aufgabe 13.5b
## [1] 0.5208333Herzliche Gratulation. Sie haben alle Übungen geschafft!
Reuse
Citation
BibTeX citation:
@online{senn2024,
author = {Senn, Mirjam and Wyssen, Gerda},
title = {Übung 13},
date = {2024-12-09},
url = {https://psylu.github.io/statistik1-hs24/pages/exercises/exercise_13.html},
langid = {en}
}
For attribution, please cite this work as:
Senn, Mirjam, and Gerda Wyssen. 2024. “Übung 13.” December
9, 2024. https://psylu.github.io/statistik1-hs24/pages/exercises/exercise_13.html.