Übung 8

Grundlagen der Inferenzstatistik
Authors
Affiliation

Mirjam Senn

Fakultät für Verhaltenswissenschaften und Psychologie, Universität Luzern

Gerda Wyssen

Fakultät für Verhaltenswissenschaften und Psychologie, Universität Luzern

Published

November 4, 2024

Aufgaben

Hinweise:

  • Die Formelsammlung zu dieser Übung finden Sie auf OLAT. Benützen Sie sie, wann immer Sie möchten.
  • Für die Berechnungen benötigen Sie einen einfachen Taschenrechner (auch gut auf dem Laptop möglich) mit dem Sie beispielsweise \(0.8^9\) ausrechnen können.
  • Die Tabelle zur Standardnormalverteilung finden Sie im Lehrbuch und unter Onlinematerialen des Verlags hier.
  • Für die Aufgaben und an der Prüfung stehen Ihnen die nötigen Ausschnitte der Tabellen zur Verfügung.


Aufgabe 8.1

Beantworten Sie die folgenden Fragen.

  1. Was ist der Unterschied zwischen einer Null- und einer Alternativhypothese?

Eine Alternativhypothese postuliert einen gewissen Effekt in der Population, z. B. durch ein Training oder ein Treatment. Die Nullhypothese behauptet die Falschheit der entsprechenden Alternativhypothesen, d.h. dass dieser Effekt in der Population nicht existiert.


  1. Was ist der Unterschied zwischen einer gerichteten und einer ungerichteten Alternativhypothese?

Gerichtete Alternativhypothesen geben die Richtung des behaupteten Zusammenhangs oder Unterschieds vor, ungerichtete Alternativhypothesen jedoch nicht. Eine gerichtete Hypothese wird in der Regel mit einem einseitigen, eine ungerichtete mit einem zweiseitigen Test überprüft.


  1. Was ist der Unterschied zwischen einer spezifischen und einer unspezifischen Alternativhypothese?

Spezifische Hypothesen geben den genauen Wert der von ihnen betroffenen statistischen Kennwerte an; unspezifische Hypothesen geben nur Wertebereiche an.


Aufgabe 8.2

Wie ist beim Nullhypothesentest nach Fisher der \(p\)-Wert zu interpretieren? Geben Sie bei jeder Aussage an, ob sie richtig oder falsch ist.

  1. \(p\) ist die Wahrscheinlichkeit, mit der die Nullhypothese wahr ist.
  2. \(p\) ist die Wahrscheinlichkeit, mit der die Nullhypothese falsch ist.
  3. \(p\) ist die festgelegte Grenze der Wahrscheinlichkeit (z. B. \(0.05\)), die bestimmt, ab wann ein Ergebnis als signifikant bezeichnet wird.
  4. \(p\) ist die Wahrscheinlichkeit für ein empirisches (oder jedes noch stärker gegen die \(H_0\) sprechende) Ergebnis unter der Annahme, dass die \(H_0\) gilt.
  5. Der \(p\)-Wert gibt die Überschreitungswahrscheinlichkeit an.
  6. \(p\) ist die Wahrscheinlichkeit, mit der ein Populationseffekt \(\mu\) gleich \(0\) ist.

a: falsch
b: falsch
c: falsch
d: richtig
e: richtig
f: falsch


Aufgabe 8.3

Wie ist die Teststärke definiert? Geben Sie bei jeder Aussage an, ob sie richtig oder falsch ist.

Die Teststärke…

  1. gibt die Wahrscheinlichkeit an, sich fälschlicherweise für die \(H_0\) zu entscheiden.
  2. gibt die Wahrscheinlichkeit an, sich fälschlicherweise für die \(H_1\) zu entscheiden.
  3. hängt von der Grösse des spezifizierten Effekts in der Population ab.
  4. entspricht der Fläche \(1-\beta\) der Stichprobenkennwerteverteilung unter der Alternativhypothese.
  5. gibt die Wahrscheinlichkeit an, einen Effekt einer vorher definierten Grösse zu finden, falls dieser tatsächlich existiert.

a: falsch
b: falsch
c: richtig
d: richtig
e: richtig


Aufgabe 8.4

Warum kann bei einer unspezifischen \(H_1\) die Wahrscheinlichkeit eines Fehlers 2. Art nicht bestimmt werden?

Bei einem Fehler 2. Art (auch Irrtumswahrscheinlichkeit \(\beta\)) wird die \(H_0\) angenommen, obwohl eigentlich die \(H_1\) richtig ist. Um die Wahrscheinlichkeit eines Fehlers 2. Art zu bestimmen, muss die Verteilung der Population, auf die sich die \(H_1\) bezieht, bekannt sein (es muss also \(μ_1\) bekannt sein). Eine unspezifische Hypothese macht aber nur die generelle Aussage, es bestehe ein Unterschied zwischen \(μ_0\) und \(μ_1\). Die Verteilung der \(H_1\)-Population – insbesondere ihr \(μ\) – wird nicht spezifiziert. So kann der Fehler 2. Art nicht berechnet werden.


Aufgabe 8.5

Ein statistisches Hypothesenpaar laute: \[H_0: μ=μ_0\] \[H_1: μ=μ_1\]

Es gelte ausserdem: \(μ_1<μ_0\). Die folgende Abbildung zeigt zwei Stichprobenkennwerteverteilungen (d.h. von zwei hypothetischen Stichproben aus einer Population), von denen eine die Nullhypothese \(H_0\) und die andere die Alternativhypothese \(H_1\) beschreibt.

  1. Welche Stichprobenkennwerteverteilung beschreibt die Null-, welche die Alternativhypothese?
  2. Was wird durch den grau gefärbten Bereich markiert?
  3. Was wird durch den blau gefärbten Bereich markiert?
  4. Wo befindet sich der Ablehnungsbereich unter der \(H_0\)?
  5. Wo befindet sich die Teststärke?

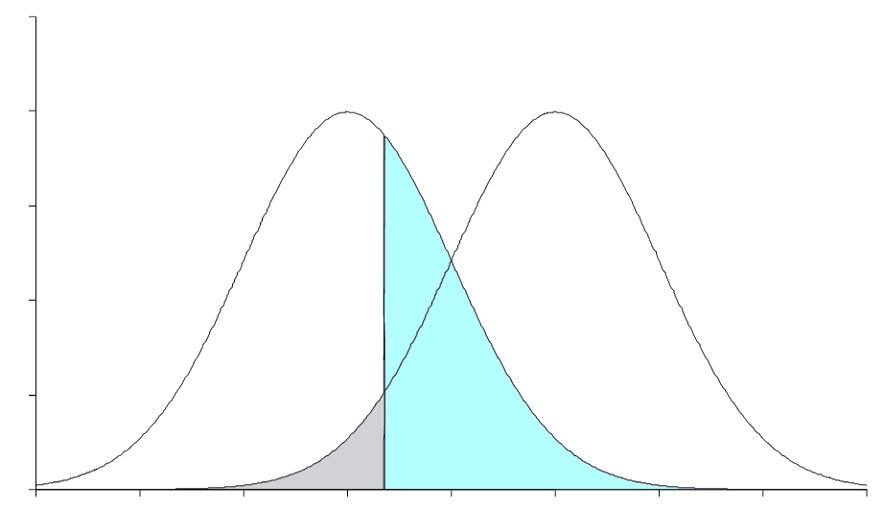
Wichtig ist zu bemerken, dass es sich hier um eine gerichtete Null- bzw. Alternativhypothese handelt; der Test wird also einseitig durchgeführt.

Der Effekt ist hier negativ, d. h. die \(H_1\) liegt unterhalb (links von) der \(H_0\). Der \(α\)-Fehler ist in der Abbildung grau gefärbt. Der \(β\)-Fehler ist in der Abbildung blau gefärbt.

Die Teststärke ist die Gegenwahrscheinlichkeit zu \(β\) unter der \(H_1\). Der Ablehnungsbereich ist der Bereich links vom kritischen Wert unter der \(H_0\).


Aufgabe 8.6

Laut neusten Forschungsbefunden kann eine Verschiebung des Unterrichtsbeginns um eine Stunde nach hinten die Lernleistung von Jugendlichen und daher deren Intelligenz steigern. Die Intelligenz wird mit einem Intelligenztest gemessen.

Eine um eine Stunde späterer Unterrichtsbeginn soll nach einem Jahr ein Anstieg um \(10\) IQ-Punkte bewirken. Der Populationsmittelwert mit herkömmlichem Schulstart liegt bei \(100\) Punkten, die Standardabweichung bei \(10\) Punkten; \(X\sim N(100,100)\). Sie testen nun nach einem Jahr eine jugendliche Person und haben einen Wert von \(x=118\) ermittelt.

  1. Formulieren Sie eine unspezifische und eine spezifische Alternativhypothese.
  • Unspezifisch: Die Verschiebung des Unterrichtsbeginns bewirkt einen Anstieg der Intelligenz.
  • Spezifisch: Die Verschiebung des Unterrichtsbeginns bewirkt einen Anstieg der Intelligenz um \(10\) IQ-Punkte.


  1. Formulieren Sie die Nullhypothese.
  • Die Verschiebung des Unterrichtsbeginns hat keinen oder einen negativen Effekt auf die Intelligenz (d.h. sie nimmt ab).


  1. Legen Sie das Signifikanzniveau fest.

Üblicherweise legen wir das Signifikanzniveau \(\alpha\) auf \(5\%\) fest, d.h. \(\alpha=0.05\).


  1. Welches ist der kritische Wert bzw. der Ablehnungsbereich unter der Nullhypothese?

\(z_{...}=_{...}\)

\(x_{krit}=_{...}\)

Wir bestimmen zuerst den \(z\)-Wert gemäss dem Signifikantniveau von \(5\%\). Dabei muss beachtet werden, ob es sich um eine gerichtete oder unberichtete Hypothese handelt. Wir testen hier eine gerichtete Hypothese (mehr IQ-Punkte).

\(z_{95\%}=1.65\)

Anschliessend berechnen wir daraus den kritischen Wert durch die Transformation in die gegebene Normalverteilung.

\(x_{krit}=\mu+z\cdot \sigma=100+1.65⋅10=116.5\)

Alle Werte gleich und über \(116.5\) liegen im Ablehnungsbereich der \(H_0\) auf dem Signifikanzniveau von \(\alpha=0.05\).


  1. Wie gross ist der \(p\)-Wert?

Der \(p\)-Wert entspricht der Überschreitungswahrscheinlichkeit und bezeichnet die Wahrscheinlichkeit, dass wir, unter der Voraussetzung dass die Nullhypothese gilt, einen Wert grösser oder gleich dem vorliegenden Testwert erhalten.

Wir ermitteln somit den \(p\)-Wert, indem wir den vorliegenden Testwert \(x\) in einen standardnormalverteilten \(z\)-Wert umrechnen und dann für diesen \(z\)-Wert bestimmen, welche Wahrscheinlichkeit alle \(z\)-Werte haben, die grösser oder gleich dem erhaltenen Wert sind.

\(z_{118}=\frac{118-100}{10}=1.8\)

\(p(z\leq 1.8)=0.9641\)

\(p(z\geq 1.8)=1-0.9641=0.0359\)


  1. Kann die Alternativhypothese angenommen werden?

Wenn Sie das Signifikanzniveau auf \(5\%\) festgelegt haben, können Sie die Nullhypothese ablehnen und die Alternativhypothese annehmen da \(p\leq a\) bzw. \(0.0359\lt 0.05\).


  1. Wie gross ist der \(\beta\)-Fehler?

Wenn wir fälschlicherweise die \(H_1\) ablehnen, bezeichnet man das als Fehler zweiter Art, die Wahrscheinlichkeit eines solchen Fehlers mit \(\beta\). Wir berechnen \(\beta\), indem wir den Flächenanteil unter der Verteilung von \(H_1\) bestimmen, der sich unterhalb des kritischen Werts zur Ablehnung der Nullhypothese befindet. Dazu rechnen wir den kritischen \(x\)-Wert unter \(H_0\) in den \(z\)-Wert von \(H_1\) um (d.h. der an derselben Stelle ist).

\(x_{krit}=116.5\) und \(\mu_1=110\)

\(z_{krit}=\frac{116.5-110}{10}=0.65\)

\(p(z\leq 0.65)=0.7422\)

\(\beta=0.7422=74.2\%\)


  1. Bestimmen Sie die Teststärke.

\(1-\beta=1-0.7422=0.2578\)

Das ergibt hier eine Wahrscheinlichkeit von \(25.8\%\), dass der Test signifikant wird unter der Annahme, dass es auch wirklich einen Effekt in der Population gibt. Die Teststärke ist hier klein, da die gerichtete Hypothese einen Unterschied von lediglich 10 IQ-Punkten postuliert, was nur einer Standardabweichung entspricht. Das heisst, es ist relativ wahrscheinlich, dass wir hier die Alternativhypothese fälschlicherweise verwerfen bzw. die Nullhypothese fälschlicherweise beibehalten, unter der Annahme, dass es einen Effekt gibt - da sich die beiden Verteilungen stark überlappen (siehe F26).


Quelle

Reuse

Citation

BibTeX citation:
@online{senn2024,
  author = {Senn, Mirjam and Wyssen, Gerda},
  title = {Übung 8},
  date = {2024-11-04},
  url = {https://psylu.github.io/statistik1-hs24/pages/exercises/exercise_08.html},
  langid = {en}
}
For attribution, please cite this work as:
Senn, Mirjam, and Gerda Wyssen. 2024. “Übung 8.” November 4, 2024. https://psylu.github.io/statistik1-hs24/pages/exercises/exercise_08.html.