Übung 2
Hinweis: Die Lösungen finden Sie in den eingeklappten Kästchen. Für einen besseren Lerneffekt bearbeiten Sie die Aufgaben zuerst ohne Hilfe, notieren die Lösungen und gleichen diese erst danach mit den untenstehenden Lösungen ab.
Aufgabe 2.1
Ein in der Statistik oft benötigtes Operationszeichen ist das Summenzeichen \(Σ\).
\[\sum_{i=1}^{5}x_i=x_1+x_2+x_3+x_4+x_5\] Diese Formel bedeutet beispielsweise, dass hier die Summe aller \(xi\)-Werte für \(i=1\) bis \(5\) berechnet wird. Der Laufindex \(i\) könnte auch durch einen beliebigen anderen Buchstaben ersetzt werden. Unterhalb des Summenzeichens wird die untere Grenze des Laufindex angegeben (hier \(1\)). Oberhalb des Summenzeichens findet man die obere Grenze. Weitere Beispiele sind:
\[\sum_{i=3}^{5}x_i=x_3+x_4+x_5\]
\[\sum_{i=1}^{3}x^2_i=x^2_1+x^2_2+x^2_3\]
Gegeben sind die fünf Werte \(x_1=1\), \(x_2=4\), \(x_3=5\), \(x_4=8\), \(x_5=10\). Berechnen Sie daraus folgende Summen:
\[\sum_{i=1}^{5}x_i\]
\[\sum_{i=1}^{5}x^2_i\]
\[(\sum_{i=1}^{3}x_i)^2\]
\[\sum_{i=1}^{5}x_i+5\]
\[\sum_{i=3}^{5}(2\cdot x_i)\]
\[\sum_{i=1}^{5}x_i=1+4+5+8+10=28\]
\[\sum_{i=1}^{5}x_i=1+16+25+64+100=206\]
\[\sum_{i=1}^{3}x_i=(1+4+5)^2=(10)^2=100\]
\[\sum_{i=1}^{5}x_i=6+9+10+13+15=53\]
\[\sum_{i=3}^{5}x_i=10+16+20=46\]
Aufgabe 2.2
Welches Mass sagt etwas über die Verteilung einer nominalskalierten Skala aus?
Mit Kennwerten der Dispersion soll angegeben werden, wie sehr sich die Merkmalsträger über die Kategorien verteilen, d.h., wie gleichmässig oder ungleichmässig die Werte der Skala vorkommen. Maximale Dispersion ist gegeben, wenn alle Kategorien gleich häufig besetzt sind, also eine Gleichverteilung der Messwerte vorliegt. Minimale Dispersion ist gegeben, wenn die Merkmalsträger sich überhaupt nicht unterscheiden, also alle den gleichen Messwert tragen. Zur Berechnung eignet sich dazu der relative Informationsgehalt H. Eine solche Berechnung müssen Sie in diesem Semester nicht durchführen können.
Aufgabe 2.3
Zwölf Studierende an der Universität Luzern wurden gefragt, welches Menü in der Mensa sie am liebsten mögen. Dies wurde auf einer Skala mit 1 = MENÜ SOUL, 2 = MENÜ VEGVEG und 3 = MENÜ BOWL erhoben.
Erstellen Sie mit den folgenden Messwerten eine Häufigkeitstabelle. Berechnen Sie die absolute Häufigkeit \(n_j\), die relative Häufigkeit \(h_j\) und die relative Häufigkeit in Anteilen von 100 (\(\%_j\)) der Merkmalsausprägungen. Überprüfen Sie Ihre Lösung bevor Sie zu Aufgabe 2.4 gehen.
| ID | Menü |
|---|---|
| 01 | 1 |
| 02 | 2 |
| 03 | 3 |
| 04 | 1 |
| 05 | 3 |
| 06 | 3 |
| 07 | 1 |
| 08 | 2 |
| 09 | 3 |
| 10 | 3 |
| 11 | 3 |
| 12 | 1 |
Beispieltabelle
| Menü (\(a_j\)) | Absolute Häufigkeit \(n_j\) | Relative Häufigkeit \(h_j\) | Relative Häufigkeit in Anteilen von 100 \(\%_j\) |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 |
| Menü (\(a_j\)) | Absolute Häufigkeit \(n_j\) | Relative Häufigkeit \(h_j\) | Relative Häufigkeit in Anteilen von 100 \(\%_j\) |
|---|---|---|---|
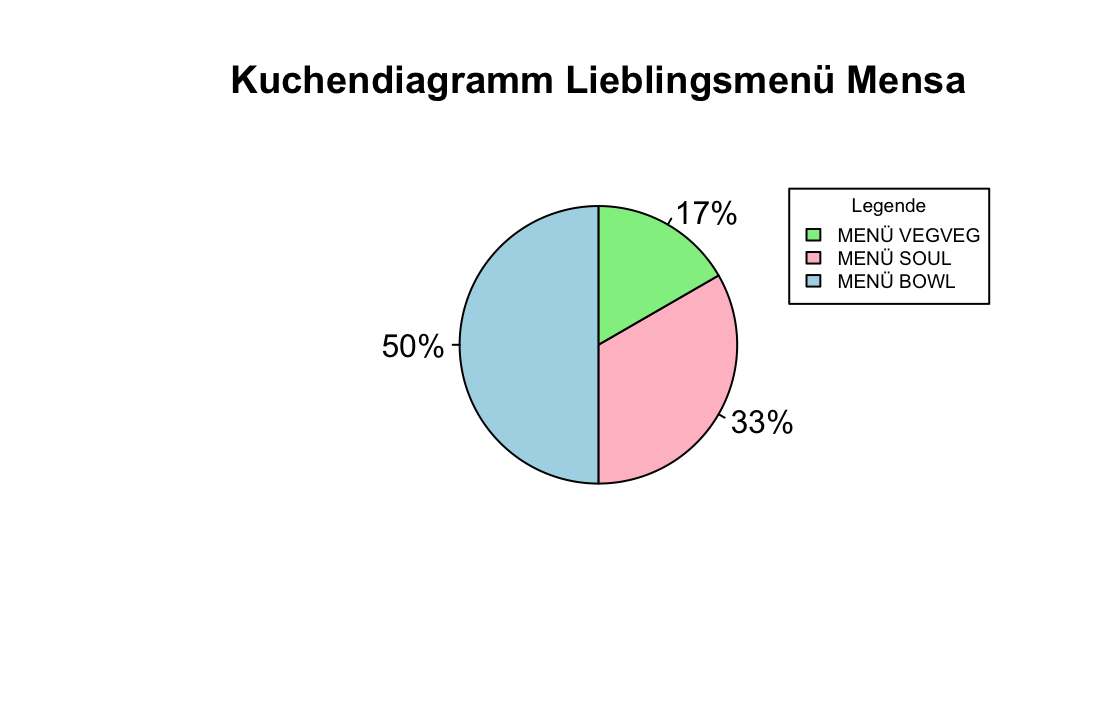
| 1 | 4 | 0.33 | 33% |
| 2 | 2 | 0.17 | 17% |
| 3 | 6 | 0.50 | 50% |
Aufgabe 2.4
Zeichnen Sie nun ein Kuchendiagramm dieser Häufigkeitstabelle. Notieren die zu den entsprechenden Segmenten die Prozentwerte und erstellen Sie eine Legende.
 So würde ein mögliches Säulendiagramm aussehen:
So würde ein mögliches Säulendiagramm aussehen: 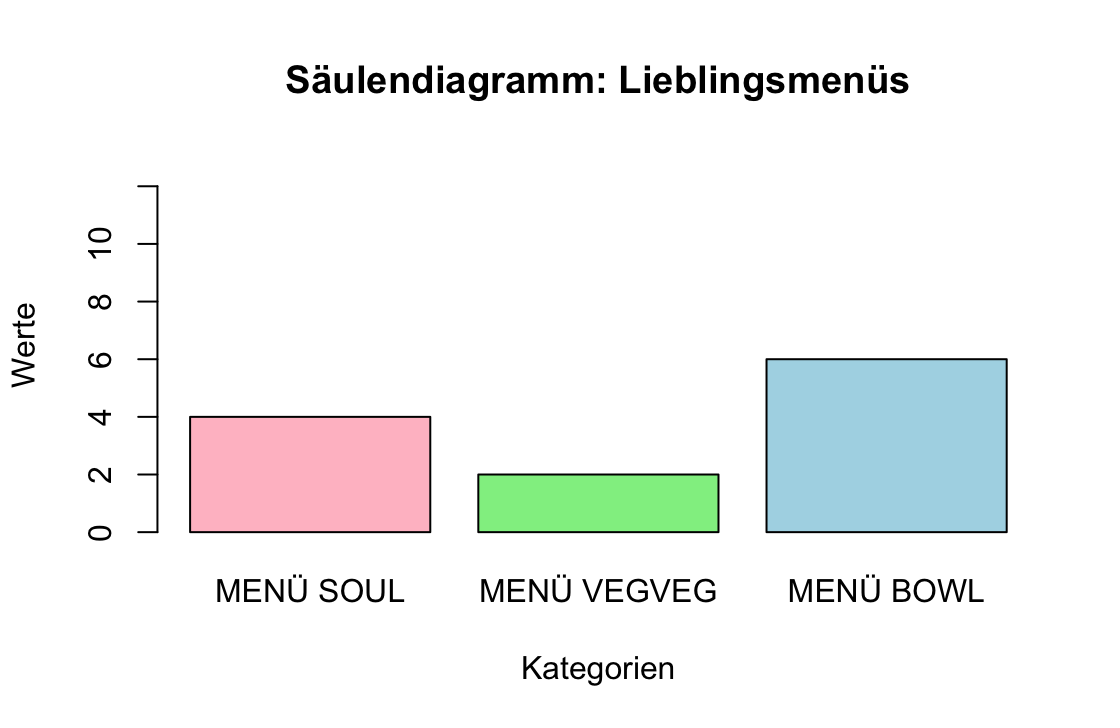
Aufgabe 2.5
Hier sehen Sie die Häufigkeitsverteilung von 24 Klient:innen über neun mögliche Persönlichkeitsstörungen hinweg.
- Bestimmen Sie den Modalwert.
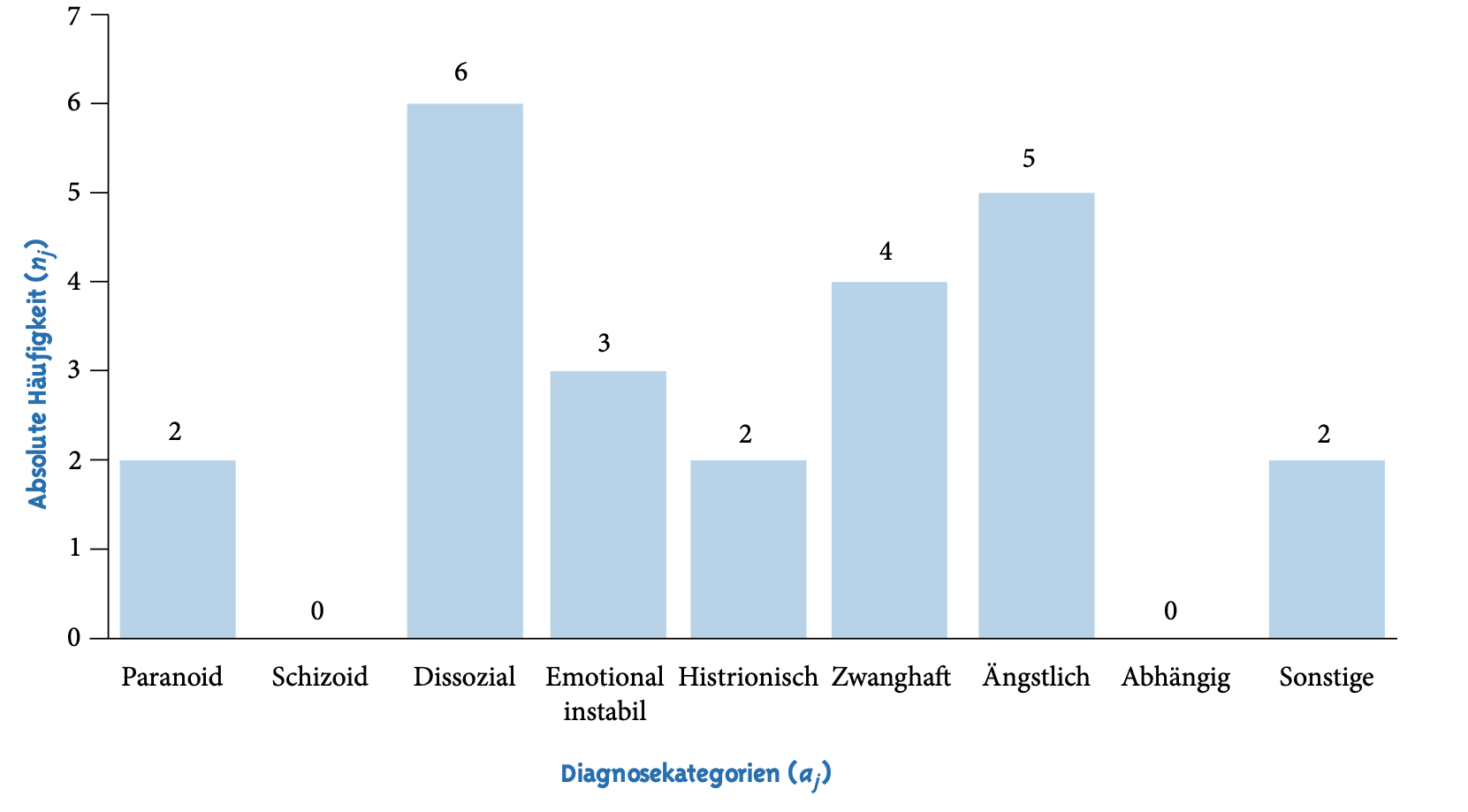
Im vorliegenden Fall ist der Modalwert Dissozial oder Dissoziale Persönlichkeitsstörung:
\(Mo=\) Dissoziale Persönlichkeitsstörung
Es wäre falsch, die Häufigkeit (6) als Modalwert anzugeben. Der Modalwert ist der Wert der Variablen (die Merkmalsausprägung) und nicht der Wert der Häufigkeit!
Ausserdem gilt: Der Modus ist dann nicht eindeutig bestimmbar, wenn jede Merkmalsausprägung nur einmal vorkommt.
- Nehmen wir an, dass eine weitere Person mit der Persönlichkeitsstörung Ängstliche Persönlichkeitsstörung dazukommt. Was verändert sich in Bezug auf den Modalwert?
Es gibt nun zwei Antwortkategorien, die gleich häufig vorkommen (ängstliche Persönlichkeitsstörung und dissoziale Persönlichkeitsstörung). Der Modus ist durch die Gleichverteilungen (Verteilungen, bei denen alle Merkmalsausprägungen mit gleicher Häufigkeit vorkommen) nicht definiert.
Der Modus reagiert sensibel auf leichte Veränderungen der Verteilung im Gipfelbereich (Gipfelverschiebungen bei ähnlich häufig besetzten Kategorien im Gipfelbereich).
Aufgabe 2.6
Die Messwerte eines Merkmals sind 7, 2, 5, 1, 10, 2, 1, 2. Welche Antworten zum Modalwert und Median sind korrekt?
- Der Modalwert ist 2.
- Der Median ist 5.
- Der Modalwert ist 5.
- Der Median ist 2.
- Der Median ist 2.5.
Korrekte Antworten: a, d
Aufgabe 2.7
Bei einem Experiment wird gemessen, wie lange die Versuchspersonen mit geschlossenen Augen auf einem Bein stehen können. Nach 21 Personen liegen folgende Messwerte in Sekunden vor.
18, 36, 18, 22, 23, 24, 26, 29, 32, 34, 36, 16, 42, 22, 43, 46, 46, 49, 57, 34, 23
- Berechnen Sie den Median.
- Berechnen Sie das untere Quartil (\(Q_1\)) und das obere Quartil (\(Q_3\)).
- Berechnen Sie den Interquartilsabstand (\(IQR\)).
Zuerst ordnen wir die Messwerte nach ihrer Reihenfolge.
16, 18, 18, 22, 22, 23, 23, 24, 26, 29, 32, 34, 34, 36, 36, 42, 43, 46, 46, 49, 57
Der Median berechnet sich durch \((n+1)/2\). Da 21 Messwerte vorliegen, liegt der Median beim 11. Messwert (Berechnung: \(22/2\)). Der 11. Messwert in der geordneten Folge beträgt 32 Sekunden.
\(Md = 32\) Sekunden
Hinweis zum Modalwert: Hier liegen mehrere Modalwerte vor (18, 22, 23, 34, 36, 46). Wir haben somit multimodale Daten, was zeigt, dass hier ein Modalwert nicht informativ ist.
Das untere Quartil (\(Q_1\)): Wir teilen dazu den Stichprobenumfang durch 4 (\(21/4=5.25\)) oder multiplizieren den Stichprobenumfang mit 0.25 (\(n\cdot 0.25 = 21\cdot0.25=5.25\)) und runden dann auf die nächste ganze Zahl (\(6\)). \(Q_1\) liegt also beim 6. Messwert, bei 23 Sekunden.
Das obere Quartil (\(Q_3\)): Wir multiplizieren dazu den Stichprobenumfang mit 0.75 (\(n\cdot 0.75 = 21\cdot0.75=15.75\)) und runden dann auf die nächste ganze Zahl (\(16\)). \(Q3\) liegt also beim 16. Messwert, bei 42 Sekunden.
\(IQR = Q3 - Q1\)
\(IQR = 42 - 23 = 19\)
Der Interquartilsabstand beträgt \(19\).
Herzliche Gratulation, alle Übungen sind geschafft!

Reuse
Citation
@online{senn2024,
author = {Senn, Mirjam and Wyssen, Gerda},
title = {Übung 2},
date = {2024-09-23},
url = {https://psylu.github.io/statistik1-hs24/pages/exercises/exercise_02.html},
langid = {en}
}